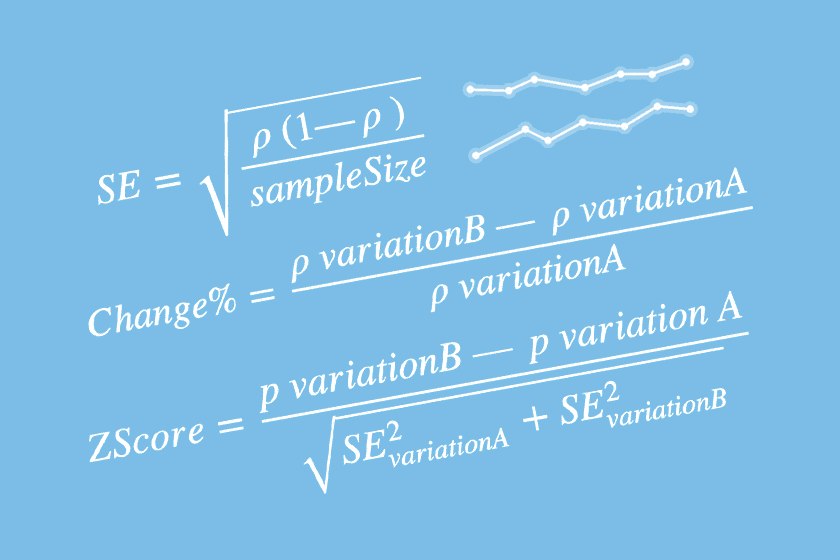How A/B Testing
Works
An Example Scenario.
Let’s say that you want to know if changing the home screen of your app in a certain way would cause more in-app purchases. One way to do this would be to measure how many customers make in-app purchases from the original home screen, then publish a new application with a changed home screen and measure how many users make in-app purchases. After gathering data for both variations of the home screen, you can decide which variation resulted in more in-app purchases. You’re 100% sure that this works because the test measured every user.
This approach has some disadvantages
- The changed home screen could have a negative impact on all of your users, resulting in fewer overall in-app purchases.
- Time-related influences, such as the time of year, sporting seasons, school holidays, competitor product releases and other factors could influence the measurements for one variation differently than the other.
- It could take a long time to measure every user for each variation.
A/B Testing Concepts
Variations
A/B testing takes two variations of a feature or promotion and distributes each version to unique groups, collecting measurements for each variation and providing measurable evidence that enables a developer to know which variation is more successful. The original state of a feature or promotion is known as the Control variation (commonly referred to as Variation A), and the new state is known as the Test variation (commonly referred to as Variation B). A/B/n Testing, a common A/B Test enhancement, allows you to test more than two Variations and can speed up testing by reducing the number of iterations required to optimize your design.
A/B testing uses statistical methods to determine whether results from a Test variation and a Control variation are different. It does this by simultaneously measuring the effect of the Control and Test variations applied to a randomly selected subset of all app users that fall into unique groups (called the Control group and the Test group(s), corresponding to the variation each receives). This method is statistically sound when a subset of users is large enough to ensure user characteristics like gender, age, location and income are proportionally the same among the subset(s) of all users of an app. In addition, provided there are enough users, the groups do not have to be equal in size as long each group has the same characteristic proportions. This solves some of the disadvantages of the initial approach:
- A smaller group of users could receive a Test variation, while the larger group receives the Control (original) variation, mitigating possible negative impacts from a test to a subset of users.
- Because all variations for a test run simultaneously, there are no time related influences outside of your control.
Confidence Intervals
The approach so far resolves the first two disadvantages noted earlier, but it doesn’t change how long it would take to measure every user — especially considering that some users may not use the app for a long time. Fortunately, from a statistical perspective, as we receive more measurements we get closer to the result of measuring everyone. With more users, we have an increasingly reasonable approximation of what we would measure if we tested everyone, but we save time by testing only a subset of users. Because it is an approximation of all users, we can estimate that the final result would fall within a certain range of values with a specific level of confidence.
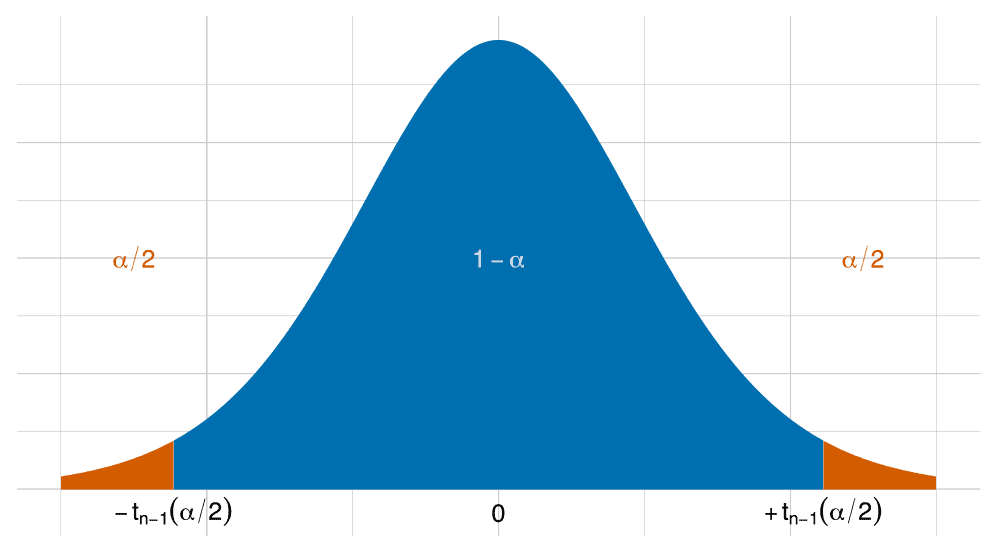
For example, we may notice that the conversion rate (the percentage of customers who make an in-app purchase) for a group of customers is somewhere in the range of 2% to 8%. This range is known as a confidence interval when we also include how confident we are of the result. The A/B Testing service uses a 90% confidence interval, so for this example we say the confidence interval is 5% ±3%. In other words, we are 90% confident the conversion rate is between 2% and 8%. As we observe more measurements, the confidence interval could get smaller.
Significance
In A/B testing, as we measure across the Control and Test groups, a confidence interval for each group’s conversion rate is calculated. The A/B Testing service also expects a minimum number of measurements in an A/B test to ensure random selection and balanced proportions. After making enough measurements, we compare the confidence interval for each group’s conversion rate and determine the chance, or likelihood, that the two results are different. The service does this by looking at the overlap of the confidence intervals for each variation. Overlap represents the potential for both variations to have the same conversion rate. If there is more than 5% overlap, then we are not confident there are enough measurements or that there is a big enough difference between the variations to conclude the Test variation will actually result in any change when compared to the Control variation. The probability of the variations being different is significance. A significance value of 95%, or 5% overlap, is a typical threshold used in A/B testing, and suggests that there is sufficient evidence that the Test variation will result in a change in the conversion rate.
Note: To learn more about the math behind A/B testing, read: The Math Behind A/B Testing
☞Arigato for reading.